Power of a Quotient
When a quotient is raised to an exponent, the result is found using the Power of a Quotient. You can divide the exponent for each factor separately if the quotient of two real numbers that are not zero is raised to an exponent.

1.) (9x)²/(y)Solution:Distribute the exponent to the terms inside the parenthesis. The given should now be:9²x²/y²Then, simplify the remaining terms until you get your final answer, which is:82x²/y²2.) (15²m²n)⁴/(3mn)Solution:First, distribute the exponent to the numbers inside the parenthesis. It should now be:15²⁽⁴⁾m²⁽⁴⁾n⁴/3⁴m⁴n⁴15⁸m⁸n⁴/3⁴m⁴n⁴Proceed with dividing the bases. With this, you will get:15 ÷ 3 = 55⁸⁻⁴ = ⁴ ᵒʳ 5⁴m⁸ – ⁴ = ⁴ ᵒʳ m⁴n⁴ – ⁴ = ⁰ ᵒʳ 15⁴m⁴(1) ᵒʳ 5⁴m⁴
Zero Exponent
When an expression's exponent is 0, the Zero Exponent is applied. When a number is raised to zero, it becomes one.

1.) (125def)⁰/( xyz )Solution:Since the whole expression is raised to the power of 0, it is now considered as 1. So the answer shall be:(125def)⁰/( xyz )
= 12.) 8²x9y10z⁰Solution:For this item, the variable z is the only term raised to 0. According to the rule, its value is now 1.8²x9y10(1)Your next step shall be simplifying the remaining terms, which is 8².8² = 8 . 8
= 64The final answer after simplifying is:64𝔁9y10
Negative Exponent
This is used when an exponent is a negative number. To transform a negative exponent into a positive one, invert the base.
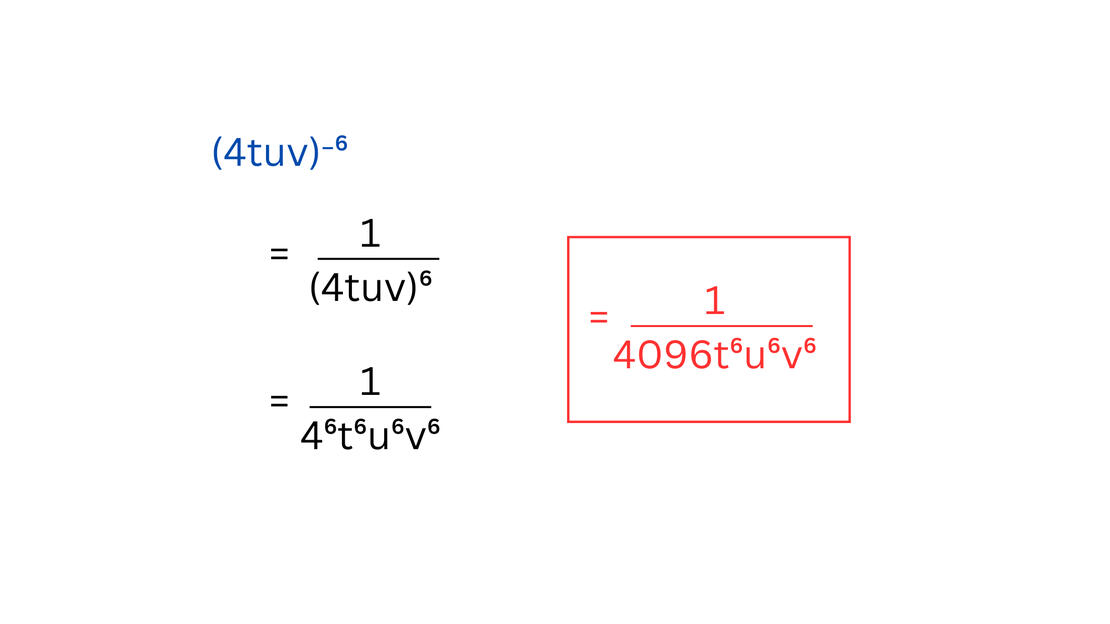
1.) (4tuv)⁻⁶Solution:Before distributing the exponent, transfer the expression to the denominator to make the exponent positive.1/(4tuv)⁶Next, distribute the exponent to the terms. It shall now be:1/4⁶t⁶u⁶v⁶Make sure to simplify your answer afterwards. The final answer should be:1/4096t⁶u⁶v⁶